先日、同僚のポスドクからテキストが届きました。
「Prism (統計ソフト) で統計やってんだけど、ANOVAでP < 0.001 ってなっているのに、Tukey では P > 0.05ってでて有意差ないって言われたんだけど、どーゆーこと!?」
送られた写真を見ると、
| Bartlett's test for equal variances | |
|---|---|
| Barlett's statistic | 18.69 |
| P value | P < 0.0001 |
| Barlett's statistic | 18.69 |
| P value summary | *** |
| Do the variances differ signif. (P < 0.05) | Yes |
となっていました。
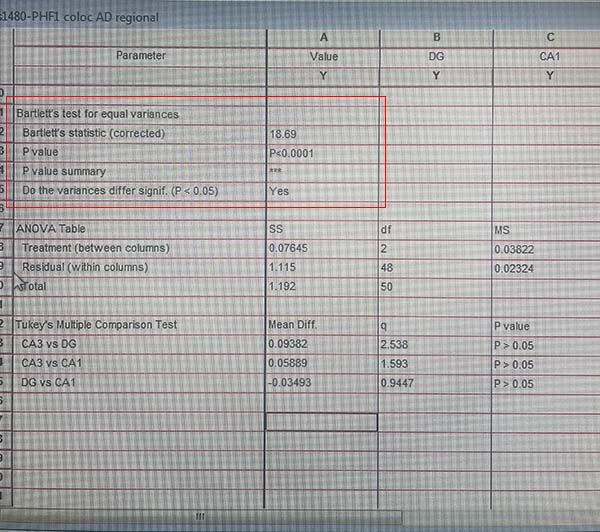
どうやら彼女は、一番上のBartlett's test の結果をANOVAの結果と思い、
「ANOVAで有意差がでたのにpost-hocで有意差が出ないのはどーゆーこと!?」
と思ったようです。
とりあえず、
「Bartlett's test は分散の均一性を検定する方法で、P < 0.05 で分散が不均一という事だから、ANOVAはしちゃいけないと思うよ。Kruskal-Wallis test と Steel-Dwass をトライ。」
と返しました。
「Thanks!!!!!」
統計を専門にしている人達からみたら驚きのやり取りかもしれませんが、アメリカのポスドクでも、ウェット系だと、統計について曖昧な感じで研究している人達がいるという事だと思います。
私も、大学の時にちゃんと統計を勉強していたわけではなく、研究を初めてから、その都度必要な部分を独学で調べていった、という感じです。
今後もし似たような事で悩んでいる人がいたときのためと、自身が色々忘れた時のために、自分の研究分野でよく登場していくる項目について、ざっくりとまとめておこうと思います。
統計手法の選択1:大まかな分類
| カテゴリー変数 | 連続変数 | 生存曲線 | ||||||
|---|---|---|---|---|---|---|---|---|
| 可視化 | 棒グラフ・箱ひげ図 etc. | ヒストグラム・棒グラフ・箱ひげ図・バイオリンプロット etc. | Kaplan-Meier 曲線 | |||||
| 分布の記述 | 度数分布 分割表 |
平均・分散・標準偏差 中央値・四分位範囲 |
||||||
群の平均値の比較 |
Fisher 正確検定 カイ二乗検定 |
正規性の検定 | シャピロウィルク検定 (Shapiro-wilk test) コルモゴロフ–スミルノフ検定 (Kolmogorov-Smirnov test) リリフォース検定 (Lilliefors test) |
|||||
| 2群 |
分散の検定 |
F検定 (F test) |
||||||
| 正規分布 | 対応なし | スチューデントのt検定 (Unpaired t-test) |
||||||
| 対応あり | 対応のあるt検定 (Paired t-test) |
|||||||
| 非正規分布 | 対応なし | マン-ホイットニーのU検定 (Mann-Whitney U test) |
||||||
| 対応あり | ウィルコクソン符号付順位検定 (Wilcoxon signed rank test) |
|||||||
3群以上 |
分散の検定 |
バートレット検定(Bartlett test) ルビーン検定(Levene test) |
||||||
| 正規分布 | 対応なし | 分散分析 (factorial ANOVA) |
log-rank 検定 | |||||
| 対応あり | 反復分散分析 (measured ANOVA) |
|||||||
| 非正規分布 | 対応なし | クラスカル・ウォリス検定 (Kruskal-Wallis test) |
||||||
| 対応あり | フリードマン検定 (Friedman test) |
|||||||
| 多変量回帰 | ロジスティック回帰 | 重回帰 | Cox 回帰 | |||||
| 共分散 | 共分散分析(ANCOVA) | |||||||
| 多変量分散 | 多変量共分散分析(MANCOVA) | |||||||
※ RStudioで始める医療統計、表8-1より一部改変
統計手法の選択2:3群以上の比較とpost-hoc
正規分布をしている2群の平均値の相違を検討するためには、t検定を用いるが、3群以上の場合は t検定を繰り返してはいけない。
3群以上の検定に t検定を使っちゃダメな理由
A-B間、A-C間、B-C間で、P value < 0.05 で有意差ありとして Student's t-testを行った場合、
「少なくとも一つが有意差あり」となる確率は、
1-(1-0.05)*(1-0.05)*(1-0.05)で計算され、P value = 0.14 となり、実際には 5%の危険率よりも甘く評価している事になる。
ANOVA(分散分析)の前提条件
- N数が十分に多い
- 分散が等しい
- 正規分布
分布に偏りがある場合は、ノン・パラメトリック検定を行う。
3群以上の比較の流れ
上記のように、
- 分散が等しく、正規分布であればパラメトリック検定
- そうでなければノン・パラメトリック検定
を行う。
| パラメトリック | ||
| 種類 | 要因の数 | 検定 |
| 要因分散分析 (factorial ANOCA) |
1要因 | 一次配置分散分析 (One-way factrial ANOVA) |
| 2要因 | 二次配置分散分析 (two-way factrial ANOVA) |
|
| 反復測定分散分析 (repeated measures ANOVA) |
1要因 | 一次反復測定分散分析 (One-way repeated measures ANOVA) |
| 2要因 | 二次反復測定分散分析 (Two-way repeated measures ANOVA) |
|
| ノン・パラメトリック | ||
| 種類 | 要因の数 | 検定 |
| 要因分散分析 | 1要因 | クラスカル・ウォリス検定 (Kruskal-Wallis test) |
| 反復分散分析 | 1要因 | フリードマン検定 (Friedman test) |
有意差が認められれば、多重比較を行う。
| 検定統計量の同時分布を利用する手法 | |
| パラメトリック | |
| 種類 | 特徴 |
| Tukey-Kramer法 | 母平均について群間ですべての対比較を同時に検定する。検出力が高く、一般的。群が多いときはBonferoniより有意差が出やすく、群が少ないときはBonferoniより有意差が出にくい。F検定の要素が組み込まれていないので、ANOVAなしでも使える。対応のある関連多群では用いることはできない。 |
| Dunnett法 | 母平均について対照群と処理群の対比較のみを同時に検定する。F検定の要素が組み込まれていないので、ANOVAなしでも使える。「対照群とその他」という比較をしたい場合は、Tukeyよりも検定回数が少ないDunnettが有意差が出やすく、こちらを選択したい。 |
| Williams法 | 母平均について対照群と処理群の対比較のみを同時に検定する。「 μ1<μ2・・・<μa 」もしくは「 μ1>μ2・・・>μa 」が想定できる場合は、DunnettではなくWilliamsを使う。 |
| Fisher's LSD法 | 多重t検定を用いる。多重性が考慮されていないので、4群以上で使用不可。ANOVAが絶対必要。 |
| Student-Newman-Keuls法 | 全ての群の平均値を大きい順に並び替え、差が大きい組み合わせから順に検出。検出力が高く、有意差が出やすい。ANOVAが絶対必要。 |
| ノン・パラメトリック | |
| 種類 | 特徴 |
| Steel-Dwass法 | 分布の位置を表すパラメータについて群間ですべての対比較を同時に検定するための順位を用いた多重比較法。Tukeyの方法のノンパラメトリック版。 |
| Steel法 | 分布の位置を表すパラメータについて対照群と処理群の対比較のみを同時に検定するための順位を用いた多重比較法。Dunnettの方法のノンパラメトリック版。「対照群とその他」という比較をしたい場合は、Steel-DwassよりもSteelを選択したい。 |
| Scheffe法 | 各群におけるすべての対比のなかで、有意なものを探す検定。有意差は出にくい。 |
| 有意水準(P値)のみを利用する手法:パラメトリック/ノンパラメトリック両方に使える | |
|---|---|
| 種類 | 特徴 |
| Bonferroni法 | 検定全体の有意水準を検定数で割る。P値に対して仮定を置かない。群が多くなると有意差が出にくく、5群以上で検出力が落ちる。F検定の要素が組み込まれていないので、ANOVAなしでも使える。対応のある関連多群で利用できる。 |
| Holm法 | P値に対して仮定を置かない。検出力はBonferroniよりも大きくなる。 |
| Hochberg法 | P値に非負の相関が見られるような仮定を置いた上でαを制御する。検出力はHolmよりも大きくなる。 |
| Hommel法 | P値に非負の相関が見られるような仮定を置いた上でαを制御する。検出力はHochbergよりも大きくなる。 |
| Sidak法 | 検出力はBonferroniと同じくらい。 |
| Simes法 | グローバルな帰無仮説に対する検定。どの帰無仮説が誤っているかまでは検出できない。 |
References
統計は何回勉強しても、すぐ忘れてしまう。一番知りたいことは、どの統計を使うかということ。 しかし、重要な点は、検定を行うのはどういうデータであるか? 得られたデータをグラフにしてみて、「比較すべきポイントは何か?」をつかむ!
多重検定 多重検定全体の説明はここからどうぞ。
1回目は,母集団,標本,母分散,母標準偏差,標本 分散,標本標準偏差,不偏分散,不偏標準偏差について 主に記述した.2回目では,パラメトリック検定の基 本,標準誤差,2群間の検定,t検定の原理,有意水準, 両側検定,片側検定,paired と unpaired t 検定の違 い,等分散性の検定,ノンパラメトリック検定の原理や 利点,欠点について述べた. 最終回は,パラメトリック検定の多重比較(3 群以上 の検定),一元配置分散分析,二元配置分散分析を中心 に記述する.
本記事では多重比較法のRでの実装を紹介する。具体的には同時分布を利用した手法(Dunnet, Tukey, Steel, Steel-Dwass法)、p値を利用した手法(Bonferroni, Holm, Hochberg, Hommel法)、グラフィカルアプローチを扱う。ただし各手法のアルゴリズムや証明については扱わない。アルゴリズムや証明については、適宜Rのドキュメントもしくは計量生物学36巻の特集等を参照することを推奨する。
この記事では、SPSSでシャピロウィルクやKolmogorov-Smirnovなどの正規性の検定を実施する方法について解
前回は 2 群データを用いて,群間の比較検定と 2 変量 データの分析について記した.今回は,群データが多数 になった場合の検定について記す.これまでの数量化や 比較検定による基礎的な統計から一歩だけ進め,研究報 告の結論に導く統計の応用についてである.
確率分布が正規分布に従うか調べたい、 二つの集団が同じ確率分布から得られたものか調べたい、 といった時に使うのが、コロモゴロフスミルノフ検定(Kolmogorov–Smirnov test) コルモゴロフ–スミルノフ検定(コルモゴロフ–スミルノフけんてい、英: Kolmogorov–Smirnov test)は統計学における仮説検定の一種であり、有限個の標本に基づいて、二つの母集団の確率分布が異なるものであるかどうか、あるいは母集団の確率分布が帰無仮説で提示された分布と異なっているかどうかを調べるために用いられる。しばしばKS検定と略される。 1標本KS検定は、経験分布を帰無仮説において示され…