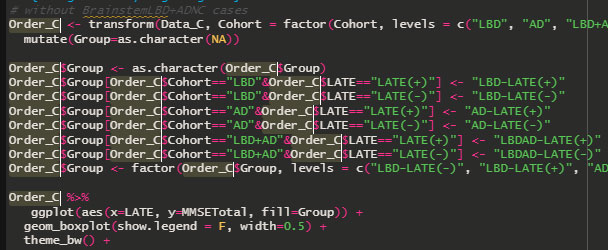
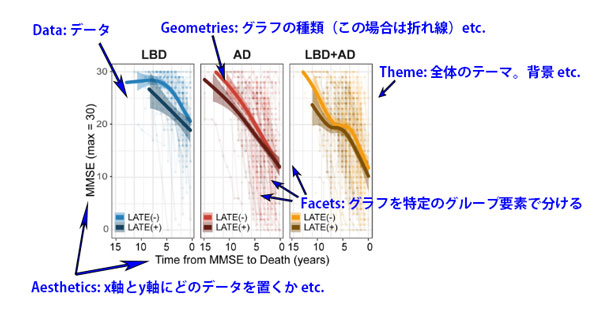
共分散分析 (analysis of covariance, ANCOVA) は、 従属変数が「連続型」の場合、1つ以上の独立変数がその連続型の共変量に影響を及ぼしているかどうか調べる時に使う。
「共変量を用いる」という点を除けば、本質的には分散分析 (analysis of variance, ANOVA) と同じ。
R で ANCOVA をする時は、「重回帰分析 + 分散分析」というイメージ。
ANCOVA を R で行う方法: 準備
ある剖検群で、生前に mini mental state examination (MMSE) の認知機能検査を行っていた。
この MMSE (スコアは 0-30 の連続型) が、
- 疾患A
- A (-)
- A (+)
- 疾患B
- B (-)
- B (+)
- MMSE 施行時の年齢 "AgeatMMSE"
- 教育を受けていた期間 "Education"
- MMSE 施行時から死亡までの期間 "MMSEtoDeath"
のうち、どのファクターの影響をうけているかを調べたい。
{tidyverse} パッケージをインストール
データ整理では必須。
install.packages("tidyverse")
library("tidyverse"){car} パッケージをインストール
install.packages("car")
library("car")Rank 関数
今回、目的変数のMMSETotalは、点数が低いほど認知機能が低下しているということ。
MMSEのデータが非正規分布だったので、今回は
rank関数で順位づけしてからモデルに投入している(データが正規分布だったらこの工程はしない)。
rank(ベクター, 昇順 or 降順, 欠損値の取り扱い方, タイの場合のランク値を返す方法)ベクター
今回は、"myData" の中の "MMSETotal" のデータを使いたいので、
myData$MMSETotalを指定。
昇順か降順か
- 昇順にランク付けしたい (最低値がランク1) 場合: asc
- 降順にランク付けしたい (最高値がランク1) 場合: desc
デフォルトは昇順。
欠損値をどのように処理するか
- "TRUE": 欠損値は最後に
- "FALSE": 欠損値は最初に
- "NA": 欠損値は削除
- "keep": 欠損値は "NA" としてランクされる
タイの場合どのように処理するか
- "ties.method=minimum": 全てのタイに対して、タイ値の最小のランク値を返す
- "ties.method=maximum": 全てのタイに対して、タイ値の最大のランク値を返す
- "ties.method=first": 最初に検出されたタイ値に対して最低のランク値を返し、次のタイは次のランク値、というようにあてがえていく
- "ties.method=random": 全てのタイに対して、ランダムにランク値を返す
- "ties.method=average": 全てのタイに対して、全てのタイのランク値の平均のランク値を返す
| 値のリスト | ties.method =minimum |
ties.method =maximum |
ties.method =first |
ties.method =average |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 2 | 2.5 |
| 3 | 4 | 4 | 4 | 4 |
| 2 | 2 | 3 | 3 | 2.5 |
| 空欄 | 空欄 | 空欄 | 空欄 | 空欄 |
| 5 | 5 | 5 | 5 | 5 |
今回、MMSEスコアは昇順、NAはキープ、タイは差が出やすいように average にランク付けしたいので、下記のように記述。
rank(myData$MMSETotal, na.last = "keep", ties.method = "average")ANCOVA を R で行う方法: "lm" と "Anova" を使う
方法は、
lm(目的変数 ~ 説明変数1 + 説明変数2 ..., データ名)で重回帰したデータを
car::Anovaで解析する。
- 目的変数: MMSE "MMSETotal"
- スコアは、0-30 の連続変数
- 説明変数1: 疾患A "A"
- A (-): ダミー変数 "0"
- A (+): ダミー変数 "1"
- 説明変数2: 疾患B "B"
- B (-): ダミー変数 "0"
- B (+): ダミー変数 "1"
- 説明変数3: MMSE 施行時の年齢 "AgeatMMSE"
- 説明変数4: 教育を受けていた期間 "Education"
- 説明変数5: MMSE 施行時から死亡までの期間 "MMSEtoDeath"
- データ: "myData"
model <- lm(rank(myData$MMSETotal, na.last="keep", ties.method = "average") ~ A + B + AgeatMMSE + Education + MMSEtoDeath, myData) %>%
car::Anova(type="II")car::Anova の type について
平方和。モデル項の仮説検定方略を指定する。
- Type I: モデル項を逐次追加し、項を追加する前と追加した後のモデルの間で比較する。モデル項を投入する順序により結果が異なる場合がある。
- Type II: 対象となるモデル項を含むモデルと、その項を要素として含む全ての項を除いたモデルとの間で比較を行う。
- Type III: すべてのモデル項を含むモデルと、対象の項を除いたモデルとの間で比較を行う。
- Type IV: データに欠損値がある場合に使う。逆にいうとそれ以外は使わない(Type III と同じ結果になる)。
要因間に順序関係がある場合は、Type I を使うのがよい。
データの分布が均等でない場合、Type I だと低次の効果から順に追加することになる(主効果、交互作用……)けれど、基本的には Type II や Type III を使用した方がよい。
Type II と Type III の選択については様々な議論があり、一概にはいえない。
私の場合、共著者が Type II を使用していたので、基本 Type II で解析を進めている。
サマリーを抽出
modeloutput
> model <- clm(as.factor(LATE_Stage_2) ~ rs5848 + Age + Female, data=Data_G)
> model <- lm(rank(Data$MMSETotal, na.last = "keep", ties.method = "average") ~ A + B + AgeatMMSE + Education + MMSEtoDeath, myData) %>% car::Anova(type="II")
>
> model
Anova Table (Type II tests)
Response: rank(Data$MMSETotal, ties.method = "average", na.last = "keep")
Sum Sq Df F value Pr(>F)
A 10675 1 13.0407 0.000456 ***
B 6504 1 7.9454 0.005694 **
AgeatMMSE 4231 1 5.1687 0.024886 *
Education 802 1 0.9798 0.324371
MMSEtoDeath 34180 1 41.7567 2.71e-09 ***
Residuals 92497 113
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
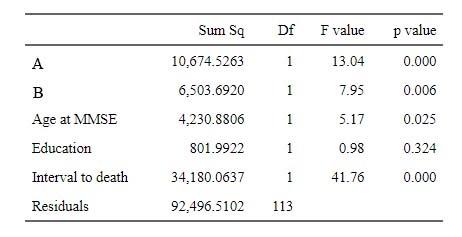
上記の結果、P value "Pr(>|Z|)" は、「疾患A」でも「疾患B」でも有意差を持って MMSE のスコアに影響している事が判明。
また、MMSE施行時の年齢や、MMSE施行時から死亡までの期間もスコアに影響している。
これは、年齢があがるほど、そして認知症疾患が進行するほど認知機能が低下するので、リーゾナブルな結果といえる。
表として出力
モデルを
as.data.frameでデータフレームに変換し、
mutateで行名を追加し、
dplyr::selectで必要な列を選出し、
mutate_atと
roundで表示する小数点を指定し、
renameで列名を変更し、
plyer::revalueで行名を変更する。
model <- model %>%
as.data.frame(row.names = row.names(model)) %>%
mutate(" " = rownames(model)) %>%
dplyr::select(` `, everything()) %>%
mutate_at(c("F value"), function(x) round(x, 2)) %>%
mutate_at("Pr(>F)", function(x) round(x, 3)) %>%
rename(p value= "Pr(>F)")
model$` ` = plyr::revalue(x = model$` `, c(AgeatMMSE = "Age at MMSE"))
model$` ` = plyr::revalue(x = model$` `, c(MMSEtoDeath = "Interval to death"))
そして、
flextableで表として出力。
model %>%
flextable::regulartable() %>%
flextable::theme_booktabs() %>%
flextable::font(fontname = "serif", part = "all") %>%
flextable::autofit()
出力結果 ▼
References
Returns the sample ranks of the values in a vector. Ties (i.e., equal values) and missing values can be handled in several ways.
式に使用できるランク関数のリストを示します。
Version 3.0-13 Date 2022-04-25 Title Companion to Applied Regression Depends R (>= 3.5.0), carData (>= 3.0-0) Imports abind, MASS, mgcv, nnet, pbkrtest (>= 0.4-4), quantreg, grDevices, utils, stats, graphics, maptools, lme4 (>= 1.1-27.1), nlme
本書はjamoviのAnalysisモードの簡易ガイドです。jamoviのAnalysisモードに含まれるメニュー項目およびその設定項目について,簡単な説明を加えています。
はじめに 2要因以上のアンバランスなデータの分散分析をする場合、平方和の計算にはいくつかの方法があります。SASのGLM procedure1では「type I」「type II」「type III」「type IV」の4種類か...
PDF | On Sep 15, 2005, 伊藤要二 and others published 分散分析における3つタイプの平方和 - Type I, II, III SS - Three types of SS in ANOVA - 伊藤要二 - KR研究会 2005年9月15日 | Find, read and cite all the research you need on ResearchGate