momの雑記帳

R logo

【Rで統計】二元配置分散分析：One-way factorial ANOVA

R R logo

二元配置分散分析の求め方。

“二元” の “２” は、「目的変数に影響を与えるかもしれない因子型の説明変数が２つある」とゆーこと。

例えば下記の例。

 

基本事項は一元配置分散分析と同じだけれど、二元配置分散分析では、どのタイプの平方和を選択するかで結果が変わってくることがある。

 

分散分析の前提条件は下記３点。

  • N数が十分に多い
  • 分散が等しい
  • 正規分布

分散はBartlett検定で、正規性はShapiro-wilk検定で。

カテゴリー変数 連続変数 生存曲線

群の平均値の比較

Fisher 正確検定
カイ二乗検定

 正規性の検定 シャピロウィルク検定
（Shapiro-wilk test）
コルモゴロフ–スミルノフ検定
（Kolmogorov-Smirnov test）
リリフォース検定
（Lilliefors test）
２群

分散の検定 F検定
（F test）
正規分布 対応なし スチューデントのｔ検定
（Unpaired t-test）
対応あり 対応のあるｔ検定
（Paired t-test）
非正規分布 対応なし マン-ホイットニーのU検定
（Mann-Whitney U test）
対応あり ウィルコクソン符号付順位検定
（Wilcoxon signed rank test）
３群以上 分散の検定 バートレット検定（Bartlett test）
ルビーン検定（Levene test）		  
正規分布 対応なし 分散分析
（factorial ANOVA）		 log-rank 検定
対応あり 反復分散分析
（measured ANOVA）
非正規分布 対応なし クラスカル・ウォリス検定
（Kruskal-Wallis test）
対応あり フリードマン検定
（Friedman test）
多変量回帰 ロジスティック回帰 重回帰 Cox 回帰
共分散 共分散分析（ANCOVA）
多変量分散 多変量共分散分析（MANCOVA）

 

二元配置以上の場合、平方和について気をつけておく 必要がある。

ANOVA を R で行う方法: 準備

パッケージをインストール

{tidyverse} パッケージ

今回の関数を使う前段階のデータ整理で必須（モデルでは使わない）。

install.packages("tidyverse")
library("tidyverse")

{car} パッケージ

３番目の手法 “Anova()” で使用。

install.packages("car")
library("car")

ANOVA を R で行う方法色々

R で ANOVA を行う用法は、いくつかあり、それぞれ少しずつ異なる。

  • aov()
  • anova()
  • car::Anova()

それぞれの関数の違い

大まかな違いは下記のような感じ。

等分散を仮定しているかどうか

  • aov(): 等分散を仮定
  • anova(): 等分散を仮定
  • car::Anova(): 等分散を仮定

平方和のタイプの選択

一元配置分散分析とは異なり、二元配置以上の分散分析の場合、この平方和の選択で結果が異なる事がある。

平方和のタイプについては後述する事にして、Rの場合は下記事項に注意。

  • aov(): Type I
  • anova(): Type I
  • car::Anova(): Type を選択できる

aov() と anova() の場合、平方和はタイプIとなっており、自由に選択できない。

これに対して、carパッケージのAnovaは、機能の中で平方和のタイプを指定できる。

aov() と anova() の違い

aov は内部に線形モデルのlm関数を含んでおり、一元時配置分散分析で使用。回帰係数、適合値、残渣などを生成する。

lm オブジェクトの拡張のような感じ。

anova() は一般的な関数で、一元配置分散分析で使用する時は、lm()やaov()でモデルを構築し、それをanova()関数に与える。

実際の使用例

今回は下記のような例でモデルを作る。

例

マウスの病理X（Pathology）の数が、ジェノタイプ（Genotype）、および何らかの薬剤処置処置（Drug）でどう変わるか調べる。

  • 目的変数(response variable)：Pathology
  • 説明変数(explanatory variable)：
    • Genotype（Tg or WT）
    • Drug（+ or -）

方法１：aov() を使う

aov() はRの標準パッケージ。平方和は Type I。

aov(目的変数 ~ 説明変数1 * 説明変数2, data = データフレーム)

のような形で使用する。

# Two-way ANOVA using aov()
model < aov(Pathology ~ Genotype * Drug, df)
summary(model)

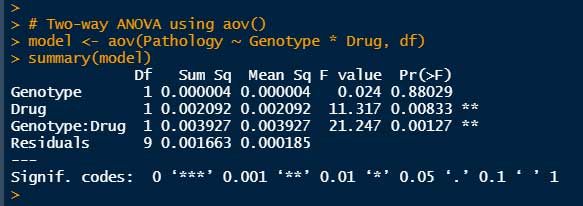
two-way-anova-1

Drugの有無（P = 0.0083）と、Drug x Genotype の交互作用（Interaction, P = 0.0013）で有意差がある、という結果となった。

方法２：anova() を使う

anova()は一般的な関数。

一元配置分散分析で使用する場合は、まずlm()やaov()でモデルを構築し、それをanova()関数に与える。

lm()を間にはさむ場合

anova(lm(目的変数 ~ 説明変数1 * 説明変数2, data = データフレーム))
# Two-way ANOVA using anova(lm())
anova(lm(Pathology ~ Genotype * Drug, df))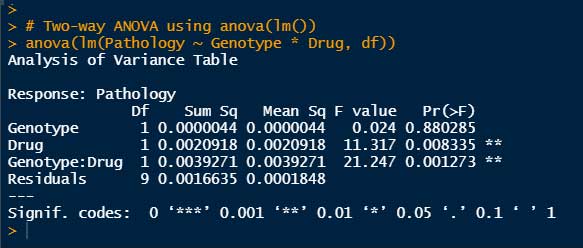

two-way-anova-2

Drugの有無（P = 0.0083）と、Drug x Genotype の交互作用（Interaction, P = 0.0013）で有意差がある、という結果となった。

aov()を間にはさむ場合

anova(aov(目的変数 ~ 説明変数1 * 説明変数2, data = データフレーム))
# Two-way ANOVA using anova(aov())
anova(aov(Pathology ~ Genotype * Drug, df))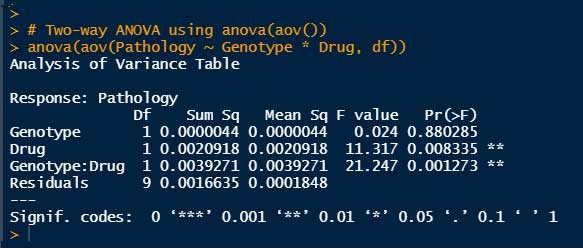

two-way-anova-3

Drugの有無（P = 0.0083）と、Drug x Genotype の交互作用（Interaction, P = 0.0013）で有意差がある、という結果となった。

方法３：car::Anova() を使う

carパッケージをインストールすると使える。

aov(), anova() と違って、平方和を指定することができる。

Type III を選択する時は、事前に設定変更が必要。

Type IIを使用、lm()を間にはさむ場合

Anova(lm(目的変数 ~ 説明変数1 * 説明変数2, data = データフレーム))
# Two-way ANOVA using car::Anova(lm()) with Type II SS
Anova(lm(Pathology ~ Genotype * Drug, df), type = 2)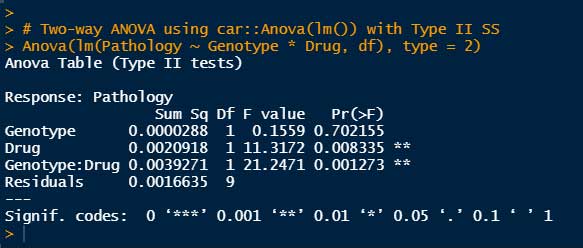

two-way-anova-5

Drugの有無（P = 0.0083）と、Drug x Genotype の交互作用（Interaction, P = 0.0013）で有意差がある、という結果となった。

Type IIを使用、aov()を間にはさむ場合

Anova(aov(目的変数 ~ 説明変数1 * 説明変数2, data = データフレーム))
# Two-way ANOVA using car::Anova(aov()) with Type II SS
Anova(aov(Pathology ~ Genotype * Drug, df), type = 2)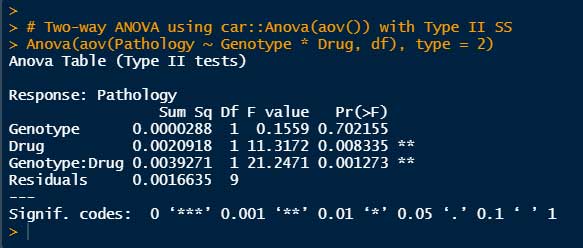

two-way-anova-5

Drugの有無（P = 0.0083）と、Drug x Genotype の交互作用（Interaction, P = 0.0013）で有意差がある、という結果となった。

Type IIIを使用、lm()を間にはさむ場合

car::Anova() で Type III を選択する場合、Rのデフォルトの設定だとダメで、Anova()の前に

options(contrasts = c("contr.sum", "contr.sum"))

でオプションを変更しておく必要があるらしい（StatsBeginner：初学者の統計学習ノートより）。

options(contrasts = c("contr.sum", "contr.sum"))
Anova(lm(目的変数 ~ 説明変数1 * 説明変数2, data = データフレーム), type = 3)
# Two-way ANOVA using car::Anova(lm()) with Type III SS
options(contrasts = c("contr.sum", "contr.sum"))
Anova(lm(Pathology ~ Genotype * Drug, df), type = 3)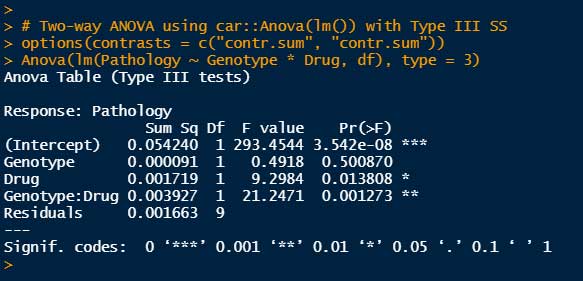

two-way-anova-８

Genotype (P = 0.019), Drugの有無（P = 0.0003）と、Drug x Genotype の交互作用（Interaction, P = 0.0013）で有意差がある、という結果となった。

Type III では切片（Intercept）も出てくるが、今回は気にしなくてOK。

Type IIIを使用、aov()を間にはさむ場合

options(contrasts = c("contr.sum", "contr.sum"))
Anova(aov(目的変数 ~ 説明変数1 * 説明変数2, data = データフレーム), type = 3)
# Two-way ANOVA using car::Anova(aov()) with Type III SS
options(contrasts = c("contr.sum", "contr.sum"))
Anova(aov(Pathology ~ Genotype * Drug, df), type = 3)

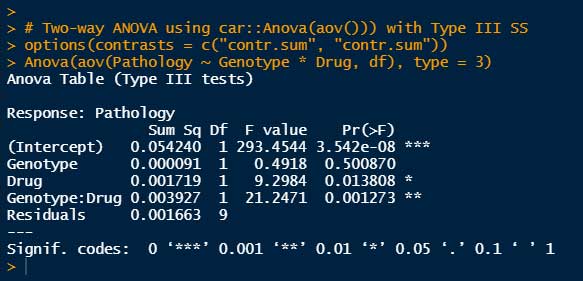
two-way-anova-9

Genotype (P = 0.019), Drugの有無（P = 0.0003）と、Drug x Genotype の交互作用（Interaction, P = 0.0013）で有意差がある、という結果となった。

Type III では切片（Intercept）も出てくるが、今回は気にしなくてOK。

 

・
・
・

 

今回は、アンバランスデータだけれども要因が直交していたので、Type I と Type II の方法では平方和、F値、P値の値が一致したが、Type III は一致しなかった（交互作用項は一致）。

平方和について

一元配置分散分析の時は問題にならなかったけど、二元配置分散分析の場合、どの平方和を選択するかで値が変わってくる事がある。

正直、完全には理解できてはいないけれど、ざっと調べた後の私の理解として、以下に書き留めておく。

平方和とは

平方和には、

  • 総平方和：応答変数の全体のバラツキ
  • モデル平方和：モデルによって説明できた応答変数のバラツキ
  • 残差平方和：モデルによって説明することができなかった応答変数のバラツキ

というイメージで、

「総平方和 ＝ モデル平方和 ＋ 残渣平方和」

という関係が成り立つ。

 

このうち、「モデル平方和」を分解する方法がいくつか提唱されており、Type I ～ Type IV までがよく知られている。

モデル平方和は、

  • 回帰分析 → 各説明変数（各説明変数）
  • 分散分析 → 各要因、交互作用項も含めて、モデル全体で説明できた応答変数のバラツキ

の事になる。

以降、この「モデル平方和」の事を、「平方和」と表す事とする。

 

例えば、要因A、要因B、それらの交互作用項 A * B で説明する分散分析モデルを考えると、

  • 要因Aが行った説明量
  • 要因Bが行った説明量
  • 交互作用項 A * Bが行った説明量

はそれぞれどれくらいと考えるか、というイメージ。

Type I 平方和

複数の変動要因の効果（主効果、交互作用）を１つずつモデルに追加していく時、モデルの平方和の増加分をその効果の平方和と考える。

  1. 最初に要因Aをモデルに組み込み、できる範囲の説明を全て行う。その量が全て要因Aがの平方和となる。
  2. 次に要因Bをモデルに組み込み、要因Aがやり残した説明の中から、できる範囲の説明を全て行う。
  3. 最後に交互作用項 A * B をモデルに組込、要因Aおよび要因Bの両方がやり残した説明の中から、できる範囲の説明を行う。

このため、ある要因の効果は、その前にモデルに投入された全ての要因の影響を受ける、という事になり、Type I の平方和は、要因の投入順序により異なった値を取る。

ただし、要因Aと要因Bで説明できる範囲が重なっていない場合、つまりデータが直行釣り合い型の場合は、どちらを先に投入してもお互いが説明する量が変わらないので、要因の投入順序の影響を受けない。

 

全ての要因のバランスが取れている場合は Type I の結果は Type II や Typa III と同じになる。

アンバランスな場合は、低次の効果から順に投入（主効果、二重交互作用、三重交互作用……）する事になるが、現実的には Type II or Type III を選択していた方が無難っぽい。

Type II 平方和

モデルはType I とほぼ同じで、Type III のような特定の仮定を必要としないが、Type I と異なり、同レベルの効果はモデルに一斉投入される。

Type IIの場合、

  1. 主効果に関しては、まず全ての要因の主効果だけを投入したモデルにおいて全体の平方和を計算する。
  2. 次にそこからある要因の主効果を取り除いたモデルの平方和を計算し、その減少分をその要因の主効果の平方和とする。
  3. 同様の手順で、全要因についての主効果が計算される。

つまり、

  • 要因Aだけでしか説明できない部分を要因Aの説明量として計算
  • 要因Bだけでしか説明できない部分を要因Bの説明量として計算
  • どちらでも説明できる部分（要因Aと要因Bが重なった部分）、および交互作用 A * B は考慮しない

という事になり、投入順序に依存しない。

Type III 平方和

Type III では、Type IIと似ているけれども、特定の仮定を必要とし（各要因内のダミー変数を足すと０になるように行列を作る）、全ての効果（要因A、要因B、交互作用項A*B）がモデルに同時投入される点が Type II と異なる。

主効果、交互作用にかかわらず、ある効果の平方和は、全効果を投入したモデルからその効果を取り除いた時の、平方和の減少分として計算される。

なので、ある効果がそれ以外の全ての効果（主効果、交互作用）でコントロールされた状態で検討されることになり、投入順序に依存しない（この点はType IIと同じ）。

 

R の car::Anova() で Type III を選択する場合で、

  • アンバランストなデザイン（セル間でサンプルサイズが異なる）
  • 交互作用あり
  • タイプIII平方和を使う

という条件の分散分析を行うときは、事前に

options(contrasts = c("contr.sum", "contr.sum"))

で設定を変更しておく必要があるらしい（StatsBeginner：初学者の統計学習ノートより）。

（試しに、オプション変更あり/なしで同じコードを流してみたら、実際に結果が異なっていた。）

Type IV 平方和

Type III の類似版で、データに空のセルが存在するときに使う。

逆に言えば、空セルのない状態ではあまり使用せず、使用した場合は Type III と同じ結果になる。

Type IV では、空のセルが存在している場合、データが存在するセルだけでできる範囲の比較を行い、そこから各要因の主効果や交互作用を推定するという方法をとる。

Type I、Type II、Type III の結果が一致する場合と一致しない場合

バランスデータの場合

Type I、Type II、Type III、全ての結果が一致する。

アンバランスなデータの場合

要因が直交していれば Type I と Type II の結果は一致するが、Type III の結果は一致しない。

要因が直交していなければ、Type I、Type II、Type III の結果は全て一致しない。

Rで分散分析をする場合の平方和の選択

Rでは

  • Rの場合、aov() や anova() 関数は Type I 平方和を使用しており、変更はできない。
  • RでType II, III…を選択したい場合は、carパッケージの Anova() 関数を使う。

どの平方和を選択するか？

  • データがバランスデータで直交釣り合い型タイプの場合は Type I を選択しても問題ないが、アンバランスなデータの場合は Type II か Type III を選択した方がよい。
  • 普段遣いは Type II と Type III で意見が分かれるところ。
  • Type III との違いとして、Type IIでは、セル内のデータ数を反映することなり、セルの間での繰り返し数が極端に違う場合は、Type III よりも Type II がいいらしい。
  • 多くの統計ソフトは Type III を選択しているらしい。

Type II と Type III のどちらを使用するかについては、様々な意見があり、結局どちらがいいのか正直よくわからない……

参考として、以下、「井関隆太のページ」より転載。

タイプⅡ タイプⅢ
モデル タイプⅠとほぼ同じ（推定順序，投入項を入れ替えたものに相当） 特定の仮定を必要とする（各要因内のダミー変数を足すと０になるように計画行列を作る）
効果の統制 自身を下位の項として含まない効果の影響のみ統制 他のすべての効果を統制
データ数の反映 セル内のデータ数を反映 データ数の少ないセルも平等に扱う

これらの特徴から，平方和の選択に関しては，以下のような指摘がなされています。

  • タイプⅢは分析の目的にとって本質的でない，特定のパラメータ制約に依存するが，タイプⅡは依存しない（Langsrud, 2003）
  • セルの間で繰り返し数が極端に違う場合は，タイプⅡの方がよい（高橋他, 1989）
  • タイプⅡの仮説検定はセル頻度に依存するので，タイプⅢの方がよい（Langsrud, 2003：ただし，著者に対立する見解として言及されている）
  • 主効果や下位の効果については，タイプⅡの方がやや検出力が高い（Langsrud, 2003; Macnaughton, 1998）

私の場合、共著者が Type II を使用していたので、基本 Type II で解析を進めている。

今度彼女に Type II を選択している理由を聞いてみようと思う。

変数の名称について

今回、目的変数、説明変数という名称を使用しているけど、下記の言葉群も同じ意味。

変数の名称色々
  1. 結果に影響を与える因子の変数
    • 説明変数（explanatory variable）
    • 独立変数（independent variable）
    • 予測変数（predictor variable）
  2. 1の影響を受けて発生した結果の変数
    • 目的変数、応答変数、反応変数（response variable）
    • 従属変数（dependent variable）
    • 結果変数（outcome variable）
    • 基準変数（criterion variable）
    • 被説明変数（explained variable）

References

StatsBeginner: 初学者の統計学習ノート
Rで平方和のタイプを選ぶ - StatsBeginner: 初学者の統計学習ノート

年末年始にやっていた実験データの分析の中で、分散分析を何回も行ったのですが、Rで分散分析をやるときに基本関数では平方和の…

StatsBeginner: 初学者の統計学習ノート
分散分析でタイプIII平方和を使う時の落とし穴（計画行列の設定） - StatsBeginner: 初学者の統計学習ノート

デフォルト設定ではダメ 先日、RでタイプIII（タイプ3）平方和を使う方法についてエントリを書いた直後に、落とし穴があっ…

riseki.php.xdomain.jp
ANOVA君/平方和のタイプ - 井関龍太のページ

分散分析をしようとするとき，思わぬ問題が生じることがあります。 要因計画の各セル内のデータ数が等しいとき（釣り合い型計画…

personal.hs.hirosaki-u.ac.jp
第9章　一元配置分散分析と多重比較法

　Rコマンダーで分散分析を行った結果は，他の統計ソフト（例えばSPSSなど）と異なることがあります．1元配置分散分析，反…

stackoverflow.com
When should I use aov() and when anova()?

I have referred to much of online literature but it is incre…

www.sas.com
glm における TypeI，TypeII および TypeIII の計算例

glm プロシジャにおける TypeI，TypeII および TypeIII 平方和の計算方法について小データを用いて例…

Rによる一元配置分散分析

Rによる一元配置分散分析の実行方法について．…

統計WEB
1-5. 説明変数と目的変数 - 統計WEB

統計学では、「説明変数」という言葉と「目的変数」という言葉が頻繁に出てきます。 例えば、バネにおもりを付けてバネがどのく…

 

 

R logo
最新情報をチェック！

Rの最新記事8件