デスクワークをしながら、久しぶりにRを開きました。
R is a free software environment for statistical computing and graphics. It compiles and runs on a wide variety of UNIX platforms, Windows and MacOS. To download R, please choose your preferred CRAN mirror. If you have questions about R like how to download and install the software, or what the license terms are, please read our answers to frequently asked questions before you send an email.
私は最初、「言語さえ理解できれば応用が利く」と思って、統計にはRを利用していたのですが、周りの同僚達は皆、ラボが購入している統計ソフトを使っているので、最近はRから少し遠ざかっていました。
上司から、臨床よりのプロジェクトを一つ任されていたので、自宅で細々解析していたのですが、ラボの統計ソフトでは解析できないものも多く、ちょっと使いづらい……。
とゆー経緯で、やっぱりRに戻ってしまったのでした。
しかしながら、久しぶりにRを開いてみると、R言語をイロイロ忘れている事に気づき、愕然としました。
これからは忘れないように、ここにメモっておこうと思います。
今回の備忘録は、ロジスティック回帰分析。
いつもは青木先生の「Rによる統計処理」にかなりお世話になっていたのですが、
第1章 Rを使ってみる 第2章 データの取り扱い方 第3章 一変量統計 第4章 二変量統計 第5章 検定と推定 第6章 多変量解析 第7章 統合化された関数を利用する 第8章 データ分析の例 付録A Rの解説 付録B Rの参考図書など
95%CIを出すときなどにちょっと不都合があったので(私の読解力不足だと思います。青木先生、ごめんなさい。)、今回は他のサイトをイロイロ参考にしながら自分で出してみました。
以下、備忘録。
Rでロジスティック回帰分析
まず、ポジティブの症例数が因子の数x10以上である事を確認。
データを取り込む。
エクセルのデータを R にインポートする方法。 csv ファイル エクセルデータを csv ファイルに保存してインポートするのが最も一般的。 CSV ファイルとは CSV ファイルは、「comma Separated V …
ちゃんと読み込めているか、最初の6行を表示する。
head(data1)
出力例:
Sex Age pathology
1 0 90 1
2 0 87 1
3 0 102 1
4 0 70 1
5 1 90 1
6 1 80 1
Rに用意されているglm関数を用いて多重ロジスティック回帰分析を行う。
> res <- glm(data1$目的変数 (pathology)~., data=data1, family=binomial)
res <- glm(data1$pathology~., data=data1, family=binomial)
もしくは
> res <- glm(data1$目的変数 (pathology)~説明変数1 (Sex)+説明変数2 (Age), data=data1, family=binomial)
res <- glm(data1$pathology~Sex+Age, data=data1, family=binomial)
そしてサマリー出力。
summary(res)
出力例:
Call:
glm(formula = data1$pathology ~ Sex + Age, family = binomial, data = data1)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5701 -0.9785 -0.7176 1.2256 1.8862
| Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -4.911966 0.720208 -6.820 9.09e-12 *** Sex 0.480557 0.173798 2.765 0.00569 ** Age 0.052668 0.009036 5.829 5.59e-09 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 |
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 830.31 on 628 degrees of freedom
Residual deviance: 781.38 on 626 degrees of freedom
AIC: 787.38
Number of Fisher Scoring iterations: 4
※ 解析結果の読み方は,基本的には線型回帰分析の場合と同じであり,「Coefficients」(赤枠)に注目すると,切片と係数の推定値(Estimate)とその標準誤差(Std. Error),P値(Pr( > |z|))を出すためのZ値(z value)が表示されている。
coefficients(res)
出力例:
(Intercept) Sex Age
-4.91196580 0.48055663 0.05266811
residuals(res)
出力例:
1 2 3 4 5 6 7 8 9
1.2512006 1.3203070 0.9892391 1.7220360 1.0494316 1.2712623 1.3874283 1.4817758 1.3640056
.....
ロジスティック回帰分析の結果の解釈
※ 線型回帰直線の場合と異なり,ロジスティック回帰分析では,得られた切片と係数の推定値に「一手間」かけないと,結果の解釈ができない。得られた推定値はexp(推定値) と変換することによって,オッズ比になる。
例えば、上記のデータの場合、Sexの推定値を入れると、Sexのオッズ比が出力される。
exp(0.480557)
出力例:
[1] 1.616975
Ageの推定値を入れると、Ageのオッズ比が出力される。
exp(0.052668)
出力例:
[1] 1.05408
Alternative: 間違いが起こらないように、解析結果resから係数をとる方が良さげ。
まず、解析結果resには何がどこに入っているか見るため、namesを入力。
names(res)
出力例:
[1] "coefficients" "residuals" "fitted.values" "effects"
[5] "R" "rank" "qr" "family"
[9] "linear.predictors" "deviance" "aic" "null.deviance"
[13] "iter" "weights" "prior.weights" "df.residual"
[17] "df.null" "y" "converged" "boundary"
[21] "model" "call" "formula" "terms"
[25] "data1" "offset" "control" "method"
[29] "contrasts" "xlevels"
1番目に係数が格納されている事がわかったので、[1]から切片と係数の推定値を出力。
res[[1]]
出力例:
(Intercept) Sex Age
-4.91196580 0.48055663 0.05266811
exp(res[[1]][2])
出力例:
Sex
1.616974
さらに、この中の1番目の切片と、2番目のSex、3番目のAgeの係数を取り出すには、それぞれ、
res[[1]][1]
出力例:
(Intercept)
-4.911966
res[[1]][2]
出力例:
Sex
0.4805566
res[[1]][3]
出力例:
Age
0.05266811
となる。
SexとAgeの係数をそれぞれオッズ比に変換するには、
exp(res[[1]][2])
出力例:
Sex
1.616974
exp(res[[1]][3])
出力例:
Age
1.05408
いっぺんに出力する場合は、
exp(res[[1]])
出力例:
(Intercept) Sex Age
0.00735801 1.61697421 1.05407975
以上から、補正後のオッズ比は、Sex: 1.61, Age: 1.05となる。
95% CIまで一度に出力する方法
resのサマリーをres1として出力する。
res1<- summary(res) res1
出力例:
Call:
glm(formula = data1$Pathology ~ Sex + Age, family = binomial, data = data1)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5701 -0.9785 -0.7176 1.2256 1.8862
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.911966 0.720208 -6.820 9.09e-12 ***
Sex 0.480557 0.173798 2.765 0.00569 **
Age 0.052668 0.009036 5.829 5.59e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 830.31 on 628 degrees of freedom
Residual deviance: 781.38 on 626 degrees of freedom
AIC: 787.38
Number of Fisher Scoring iterations: 4
res1の内容の中から、coefficientを取り出す。
coe <- res1$coefficient coe
出力例:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.91196580 0.720208376 -6.820201 9.091330e-12
Sex 0.48055663 0.173797974 2.765030 5.691754e-03
Age 0.05266811 0.009035981 5.828710 5.585755e-09
オッズ比とオッズ比の95%信頼区間を出力する。
- オッズ比(OR)
- オッズ比の95%信頼区間(max: ORhigh, min: ORlow)
OR <- exp(coe[,1]) ORlow <- exp(coe[,1]-1.96*coe[,2]) ORhigh <- exp(coe[,1]+1.96*coe[,2])
後から確認しやすいように、3つをまとめておく。
res2 <- cbind(coe,OR,ORlow,ORhigh) res2
出力例:
| Estimate | Std. Error | z value | Pr(>|z|) | OR | ORlow | ORhigh | |
| (Intercept) | -4.91196580 | 0.720208376 | -6.820201 | 9.091330e-12 | 0.00735801 | 0.001793522 | 0.03018659 |
| Sex | 0.48055663 | 0.173797974 | 2.765030 | 5.691754e-03 | 1.61697421 | 1.150173272 | 2.27322758 |
| Age | 0.05266811 | 0.009035981 | 5.828710 | 5.585755e-09 | 1.05407975 | 1.035575787 | 1.07291435 |
以上から、補正後のオッズ比と95%CIは、Sex (COR, 1.62; 95%CI, 1.15-2.27), Age (COR, 1.05; 95%CI, 1.04-1.07)となる。
四捨五入
上記表だと見にくいので、round関数で、P valueは小数点3桁、OR 等は小数点2桁表示にする。
OR <- round(exp(coe[,1]), 2) ORlow <- round(exp(coe[,1]-1.96*coe[,2]), 2) ORhigh <- round(exp(coe[,1]+1.96*coe[,2]), 2) res2 <- round(cbind(coe,OR,ORlow,ORhigh), 3)
表にする
見やすいように、表で出力する。
データ整理
1. データをデータフレームに変更。
res2 <- res2 %>% as.data.frame(row.names = row.names(Data1))
%>%
パイプでつないで、
2. 行名を追加。
mutate(" " = rownames(res2))
%>%
パイプでつないで、
3. いくつかの列名を見やすいように変更。
rename("P value" = "Pr(>|z|)", SE = "Std. Error")
%>%
パイプでつないで、
4. 行名の列を左側に移動。
(" ", "Estimate", "SE", "z value", "P value", "OR", "ORlow", "ORhigh")
表を作成
flextableパッケージのregulartableを使う。
res2 %>% flextable::regulartable() %>% flextable::theme_booktabs() %>% flextable::font(fontname = "serif", part = "all") %>% flextable::autofit()
自分用プログラム
上記の内容をまとめて、時短の為にプログラムを作成。
- 目的変数:Y
- 説明変数:X1, X2
として入力。
data1 <- read.table(“clipboard”,header=TRUE)
head(data1)
としてデータを取り込んだ後で、
res <- glm(data1$Y~., data=data1, family=binomial)
res1<- summary(res)
res1
coe <- res1$coefficient
coe
OR <- round(exp(coe[,1]), 2)
ORlow <- round(exp(coe[,1]-1.96*coe[,2]), 2)
ORhigh <- round(exp(coe[,1]+1.96*coe[,2]), 2)
res2 <- round(cbind(coe,OR,ORlow,ORhigh), 3)
res2 <- res2 %>%
as.data.frame(row.names = row.names(Data1)) %>%
mutate(" " = rownames(res2)) %>%
rename("P value" = "Pr(>|z|)", SE = "Std. Error") %>%
select(" ", "Estimate", "SE","z value", "P value", "OR", "ORlow", "ORhigh")
表で出力する場合
res2 %>% flextable::regulartable() %>% flextable::theme_booktabs() %>% flextable::font(fontname = "serif", part = "all") %>% flextable::autofit()
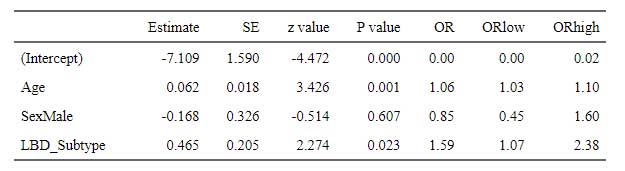
出力値の解釈:
- P値:Pr(>|z|)
- オッズ比:OR
- 95%CI:ORlowーORhigh
出力された表の例 ▼
References
今回はRによるロジスティック回帰分析の方法をご紹介します。また、「ロジスティック回帰分析をして、必要なデータを抽出しファイルに書き出す」までの一連の流れを自作関数にまとめたので、解析をお急ぎの方はそちらも参考にして頂ければ幸いです。
今回はRを用いた場合のオッズ比の求め方を記述しておく。 (オッズ比がで求めることができることを知っていれば、簡単に理解できる。) はじめに 医学研究を行う上で、なんらかの指標で群分けしたグループでのある事象のおこりやすさ(オッズ)を比較することがある(オッズ比)。今回はRを用いた場合の簡単なORの求め方を記述する。 なお、模擬データは本記事の末尾に記述するので参照されたい(ランダムで乱数を発生させているので、同じ結果にならないことに注意。) 簡単にデータのプレビューをする。 head(Ndtnew) # age gender height weight BMI alcohol ID BMI01…