
カイ二乗検定とは
カイχ二乗検定というと、一般にピアソンのカイ二乗検定を指す事が多い。
仮説によって、適合度検定や独立性の検定などがある。
基本はt検定と似ているけれど、t検定が「2つの群の連続変数(numerical variable)の平均値の比較検定」(帰無仮説(null hypothesis)は、「平均値に差がない」)を検証するのに対して、
カイ二乗検定は「2群間のカテゴリカル変数(categorical variables)の比較検定」(帰無仮説(null hypothesis)は、「相関がない」)を検証する。
カイ二乗検定は、Yes/No で表されるようなカテゴリカル変数同士の相関をみる場合などによく使われる。
2群間のカテゴリカル変数の比較検定だと、
- カイ二乗検定
- フィッシャーの正確確率検定
の2つが挙げられるが、カイ二乗検定は近似したP値を算出するのに対して、フィッシャーの正確確率検定は直接計算したP値を算出する。
カイ二乗検定とフィッシャーの正確確率検定の使い分け
基本的にはほぼ同じ値にあるけれども、サンプル数の少ない研究では、カイ二乗検定とフィッシャーの正確確率検定との誤差が大きくなる。
一般的に、2x2表のとき、
- 症例数が20例以下の場合
- または症例数が40以下で隠せるの期待値が5以下のマスが存在する場合
には、フィッシャーの正確確率検定を選択した方がよいとされている。
カイ二乗検定を行う
必要なパッケージのインストール
カイ二乗検定は、R標準パッケージの
chisq.test()で求める事ができる。
それ以外にも、データ整理で下記パッケージがあると便利。
{dityverse} パッケージ
データ整理ではほぼ必須。
install.packages("tidyverse")
library(tidyverse){epitools} パッケージ
上記のようなテーブル型のデータをデータフレームに展開する時、便利。
install.packages("epitools")
library(epitools){flextable} パッケージ
検定結果を表として出力するため。
install.packages("flextable")
library(flextable){webshot} パッケージ
最終的に出てきた表を画像として出力する時に必要。
install.packages("webshot")
library(webshot)独立性の検定
2つの観察(カテゴリ変数)に関連性があるか(or 互いに独立か)どうかを検定する。
計算値はエクセルでも簡単に計算できるけど、
オッズ比とP値はエクセルで計算可。 X1 X2 Total Y1 a b a+b Y2 c d c+d Total a+c b+d a+b+c+d 上記のようなデータがあった場合、期待値は、 期待値 X1 X2 Tota …
今回は、Rで行う方法。
治療法Xの効果が疾患Yの発症に影響があるかどうかを調べる
| 治療法Xあり | 治療法Xなし | |
| 疾患Y発症あり | 15 | 35 |
| 疾患Y発症なし | 450 | 620 |
データ準備
今回は練習を兼ねて、上記例のクロス集計表作成から。
1.2x2のマトリックスを作る。
# 2x2のマトリックスを作る
x <- matrix(data=c(15, 620, 485, 655), byrow=TRUE, nc=2)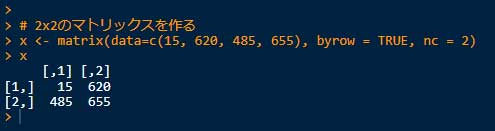
2.それぞれの項目に "dimnames" を指定する。
# dimnamesを指定する
dimnames(x) <- list(c("Yes", "No" ), c("Yes", "No" ))
names(dimnames(x)) <- c("Disease", "Treatment" )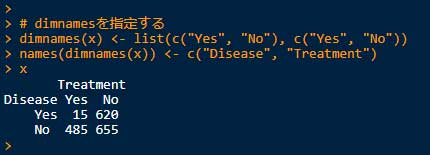
カイ二乗検定:独立性の検定
独立性の検定は、
chisq.testの因数xに分割表を表す行列またはデータフレームを代入する
chisq.test(x)か、引数xとyにそれぞれのベクトルを代入する。
chisq.test(x, y)マトリックスを代入する場合
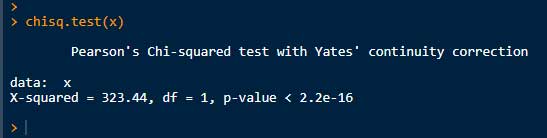
# カイ二乗検定:独立性の検定、マトリックスを使う場合
chisq.test(x)
データフレームとして代入する場合
# カイ二乗検定:独立性の検定、データフレームを使う場合
chisq.test(data.frame(x))

x, y のベクトルを代入する場合
クロス集計表を、
epitools::expand()でx,yのデータフレームに展開する。
# 2x2のマトリックスを作る
x <- matrix(data=c(15, 620, 485, 655), byrow=TRUE, nc=2)
# dimnmaes etc. を指定
dimnames(x) <- list(c("Yes", "No"), c("Yes", "No"))
names(dimnames(x)) <- c("Disease", "Treatment")
# データフレームに展開
df <- expand.table(x)
df
# 確認
head(df)2列のデータフレームに変換された。
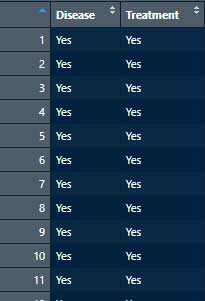
※ epitools::expand() でデータフレームに展開するためには、それぞれのセルに dimnames を指定しておく必要がある。
で、これを
chisq.test()に代入。
# カイ二乗検定、データフレーム
chisq.test(df$Treatment, df$Disease)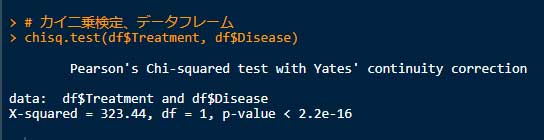
上記の結果は、いずれも P < 2.22-16 となっており、「Treatment と Disease の分布は独立ではない(つまり関係がある)」といえる。
P値以外のパラメーターにアクセスする方法
# カイ二乗検定、結果をlistに代入
Res <- chisq.test(df$Treatment, df$Disease)
# 検定統計量
Res$statistic # もしくは Res[["statistic"]]
# 自由度
Res$parameter # もしくは Res[["parameter"]]
# P値
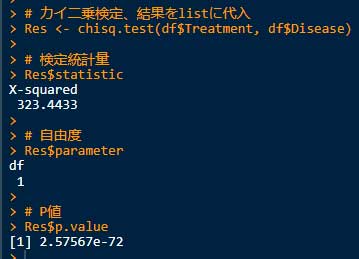
Res$p.value # もしくは Res[["p.value"]]
- カイ二乗値: 323.4
- 自由度: 1
- P値: <0.001
という結果が得られた。
表として出力
出力結果を
as.data.frameでデータフレームに変換し、
dplyr::mutateで行名を追加し、
dplyr::selectで列を並び替える。
# データフレームに
Res2 <- as.data.frame(c(Res$statistic, Res$parameter, Res$p.value, Res$method, Res$data.name))
colnames(Res2) <- "Chi square test"
Res3 <- Res2 %>%
as.data.frame(row.names = c("statistic", "parameter", "p.value", "method", "data name")) %>%
mutate(" " = rownames(Res3)) %>%
select(" ", everything()){flextable}で表として出力する。
# 表にする
Res3 %>%
flextable::regulartable() %>%
flextable::theme_booktabs() %>%
flextable::font(fontname = "serif", part = "all") %>%
flextable::autofit()
docxで保存する場合は、
flextable::save_as_docxを使用。
私は出力場所を "Export" という別フォルダにまとめたいので、下記のように出力。
# docx で保存
save_as_docx(Res3, path = "Export/Chi_square_test.docx", zoom = 3, expand = 10, webshot = "webshot")
write.csvや
readr::write_csvを使って、csv で保存してもOK。
私は出力場所を "Export" という別フォルダにまとめたいので、下記のように出力。
# cvs で保存
write_csv(Res3, "Export/Chi_square_test.csv")
カテゴリカルの要素が3つ以上の場合
上記例では2x2の分割表で表されているけど、2つの群がカテゴリカルであれば、要素は3つ以上でも適応できる。
AD neuropathologic change (ADNC) の病理所見の程度が、生前の認知症の有無に影響があるかどうかを調べる
| ADNC-Not | ADNC-Low | ADNC-Medium | ADNC-High | |
| 認知症あり | 0 | 5 | 100 | 250 |
| 認知症なし | 150 | 200 | 15 | 0 |
検定の方法は2x2の時と同じ。
1.2x4のマトリックスを作る。
# 2x4のマトリックスを作る
x <- matrix(data=c(0,5,100,250,150,200,15,0),byrow=TRUE,nc=4)
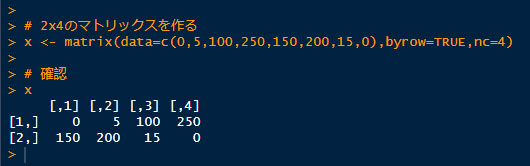
2.それぞれの項目に "dimnames" を指定する。
# dimnamesを指定する
dimnames(x) <- list(c("Yes","No"),c("Not","Low","Int","High"))
names(dimnames(x)) <- c("Dementia","ADNC")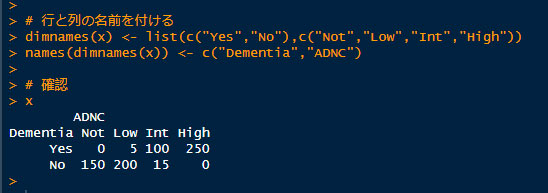
3.カイ二乗検定
# Chi二乗検定
chisq.test(x)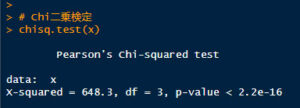
結果は P < 2.22-16 となっており、「Dementia と ADNC の分布は独立ではない(つまり関係がある)」といえる。
適合度検定
「適合度」とは、想定している分布と、実際の測定結果の一致度の事。
例えばサイコロを60回振った場合、通常なら、1の目がでる回数は10回(1/6の確率)だけど、もしサイコロに仕掛けがしてあって、20回とか30回とかでてたら、「適合度が悪い」という事になる。
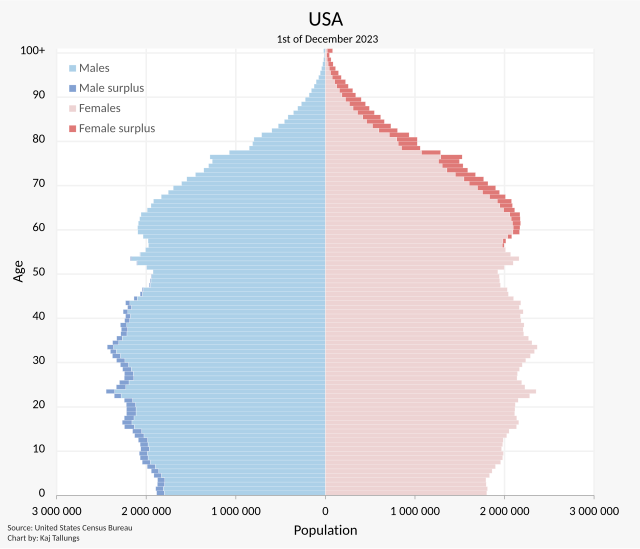
当院のコホートの人種の割合が、アメリカ全体の人種の割合と適合性があるかどうか調べる。
当院の手持ちのコホートデータでは、白人(205人)・黒人(26人)・ヒスパニック/ラテン系 (25人)・アジア系 (5人)・その他(15人)。
アメリカ全体の人種の割合は、白人(~61.5%)・黒人(~12.3%)・ヒスパニック/ラテン系 (~17.6%)・アジア系 (~5.3%)・その他(~3.3%)。
| 白人 | 黒人 | ヒスパニック/ラテン系 | アジア人 | その他 | |
| 手持ちのコホート | 205人 | 26人 | 25人 | 5人 | 15人 |
| アメリカ全体 | 61.5% | 12.3% | 17.6% | 5.3% | 3.3% |
データ作り
上例のデータを作る。
# cohortの人種別人数
cohort <- c(205, 26, 25, 5, 15)
# アメリカ全体の人種比
USA <- c(0.615, 0.123, 0.176, 0.053, 0.033)
カイ二乗検定:適合度検定
chisq.test(x = 観測度数, p = 理論分布)で求められる。
# 適合度検定
chisq.test(x = cohort, p = USA)
結果は、
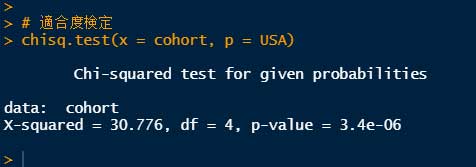
P = 3.4e-06 で、仮説は否定された。
とゆーことで、今回のコホートはアメリカ全体の人種の分布と異なる、という結果になった。
表として出力
chisq.test()を res に代入し、それぞれのパラメーターを見てみる。
# 適合度検定
res <- chisq.test(x=cohort, p=USA)
# それぞれのパラメーター
res$statistic
res$p.value
res$parameter
res$method
res$data.name
res$observed
res$expected
res$residuals
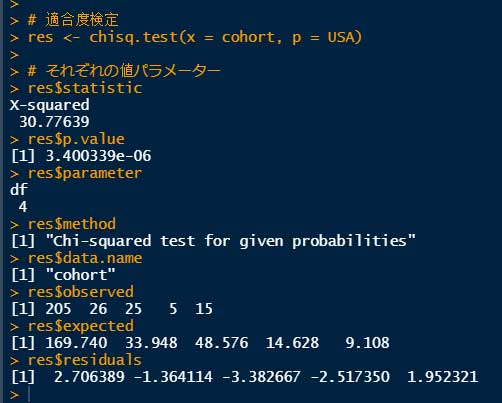
この結果を、
{flextable}を使って表として出力してみる。
# データフレームにする
res2 <- as.data.frame(c(res$statistic, res$p.value, res$parameter, res$method ))
colnames(res2) <- "chi-square goodness-of-fit test"
res3 <- res2 %>%
as.data.frame(row.names = c("statistic",
"p.value",
"parameter",
"method"
)) %>%
mutate(" " = rownames(res3)) %>%
select(" ", everything())
# 表にする
res3 %>%
regulartable() %>%
theme_booktabs() %>%
font(fontname = "serif", part = "all") %>%
autofit()
# docxで保存
save_as_docx(res3, path = "Export/chi_square_goodness_of_fit_test.docx", zoom = 3, expand = 10, webshot =
"webshot")
# csv で保存
write_csv(res3, "Export/chi_square_goodness_of_fit_test.csv")

References
こんにちは、usaig-sanです。今回はR言語でカイ2乗検定を実行する方法を解説していきます。データセットの用意から検定までの一連の流れを紹介していきます。カイ2乗検定の種類として適合度検定や独立性の検定がありますが、R言語に標準で実装されている関数を用いれば、これらの検定を統一的かつ簡単に実行することができます。
「カテゴリカルデータの解析」についてチュートリアル を行う. 2×2の分割表についてのカイ2乗検定とフイッ シャー(Fisher)の正確検定,k×2分割表についてのコ クラン・アミテージ(Cochran-Armitage)検定と ウイルコク ソン(Wilcoxon)検定,k×l分割表についての順位相関 (Spearman Kendall)係数,ヨンキー(Jonckheere)検定, 対応のある順位カテゴリカルデータについてのウイル コクソン検定等の標準的なカテゴリカルデータの解析 法について解説を行う.
カイ2乗検定は、質的変数(カテゴリカルな文字型変数や数値変数)の値の数をカウントして値の出現頻度(度数)を集計し、「そこで集計されている集計表が特異な結果ではなく、データ全体に対しても起こりうることなのか?」を検定する分析です。ノンパラメトリック検定に分類されますので、データが正規分布である必要はありません。
こんにちは。統計ブロガーのにっしーです。この記事を読むと、以下のことが分かるようになります! この記事を読むと分かること ...
R にてカイ二乗検定 (chi-squared test) を行う.カイ二乗検定とは帰無仮説が正しい場合において,対象となる検定統計量がカイ二乗分布に従う検定法全般のことをいう.しかし,一般にカイ二乗検定といえば,ピアソンのカイ二乗検定 (Pearson chi-squared test) を指す場合が多い.ピアソンのカイ二乗検定は得られたデータが特定の分布と相違があるかどうかを検定する適合度検定 (test of goodness of fit) と2つの変数について得られたデータから,それらの変数間に独立性が成立するかどうかを検定する独立性検定 (test of independence) のふたつに細分化される.独立性検定に関して,フィッシャーの直接確立検定も同様の検定を行うが,分割表 (contingency table) のマスの期待値が全て10以上である場合はカイ二乗検定で行なっても良い.カイ二乗検定はデフォルトのパッケージに含まれる関数 chisq.test() にて実行できる.
本書は大学に入学して初めて統計学を学ぶ学生、大学に進学を目指す高校生、ビジネスなどの処分やでデータ分析をしている社会人のために書かれた書籍である。




カイ二乗検定2×3の方法がいまいちわかりません。
2×2と同様とのことですが, 実際にやってみてあまりわからなかったので
例を紹介して解説していただけると助かります。
すみません、しばらくブログを開いておらず、返信が遅くなりました。
また時間が取れたときに記事を更新させてもらいます。
遅くなってすみません。既に2x4を例に出していたので、それを使った方法を追記しました。