【Rで統計】正規分布とrnorm, dnorm, pnorm, qnorm

Rを使った正規分布関連の覚書。

正規分布 (normal distribution) とは

正規分布とは、平均値と最頻値・中央値が一致し、それを軸として左右対称となっている確率分布。

多くの統計的手法において、データが正規分布に従うことを仮定している。

• 正規分布の特徴
  • 紡錘形
  • 左右対称
  • 平均値と中央値が中央で一致している
  • 「平均」と「分散」が重要
• 正規分布の68-95-99ルール
  • 約68％のデータは±1SD以内
  • 約95％のデータは±2SD以内
  • 約99％のデータは±3SD以内

以下は、偏差値 (0点から100点のテスト、平均 50、標準偏差10)の正規分布▼

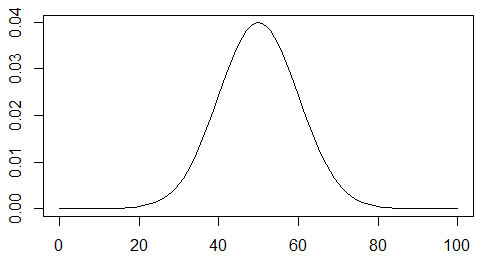
描き方は、

curve(dnorm(x, mean = ○○, sd = ○○), from = ○○, to = ○○)

で。

# 0点から100点のテスト、平均50、標準偏差10の偏差値のグラフ
curve(dnorm(x, mean = 50, sd = 10), from = 0, to = 100)

rnorm：正規分布の無作為抽出

rnormは、正規分布からランダムに値を抽出する。

例えば、平均値50で標準偏差が10の正規分布から5個の数字を無作為に抽出する場合。

# 平均値50で標準偏差が10の正規分布から5個の数字を無作為に抽出
rnorm(5, mean = 50, sd = 10)

output
> rnorm(5, mean = 50, sd = 10)
[1] 46.16207 48.85408 62.08255 54.45694 27.53638

平均値と標準偏差を指定しない場合は、-1 から 1 の正規分布 (標準正規分布: 平均 = 0, 標準偏差 = 1)になる。

# 平均値50で標準偏差が10の正規分布から5個の数字を無作為に抽出
rnorm(5)

output
> rnorm(5)
[1] -0.46152128 1.33902697 -0.37063174 -0.03551792 0.45226065

dnorm：正規分布の確率密度関数

以下、偏差値 (平均値50、標準偏差10)を使って検証。

例えば偏差値70の人の確率密度関数は、

# 偏差値70の人の確率密度関数
dnorm(70, mean = 50, sd = 10)

output
> dnorm(70, mean = 50, sd = 10)
[1] 0.005399097

pnorm：正規分布の累積分布関数

pnormは、正規分布における任意の値以下(または以上)の確率を求める。

例えば、偏差値70以下の人がいる確率は、

# 偏差値70以下の人がいる確率
pnorm(70, mean = 50, sd = 10)

output
> pnorm(70, mean = 50, sd = 10)
[1] 0.9772499

「~97.7%人は偏差値70以下」という結果が得られた。

pnormのデフォルトは "lower.tail = TRUE" なので、"○○以下" を求める事になる。

"○○以上" を求めたい場合は、"lower.tail = FALSE" にする。

# 偏差値70以上の人がいる確率
pnorm(70, mean = 50, sd = 10, lower.tail = FALSE)

output
> pnorm(70, mean = 50, sd = 10, lower.tail = FALSE)
[1] 0.02275013

「~2.3%人は偏差値70以上」という結果が得られた。

qnorm：パーセンタイル値

qnorm は pnorm の逆バージョン。

正規分布の確率を使って、パーセンタイル値を求める。

# 0.9772499の確率の人たちは偏差値いくら以下？
qnorm(.9772499, mean = 50, sd = 10)

output
> qnorm(.9772499, mean = 50, sd = 10)
[1] 70.00001

偏差値70以下の人たちが97.7%、という結果が得られた。

References